Äänioppi 1

Yläsävelsarja

Tarkastellaan äänen syntymistä kitaran kielessä. Ensinnäkin kieli värähtelee koko pituudeltaan (kts. vasen kuva). Tästä värähtelystä syntyy yksi taajuus (oikeanpuoleinen kuva).

Tällainen yhden taajuuden värähtelyn muodostamaa ääntä kutsutaan siniääneksi matematiikasta tutun sini-funktion mukaan. Muistattehan varmaan ne trigonometrian ympyrälaskut: sinit, kosinit ja tangentit - sieltä tämä nimi on peräisin, ei sinisestä väristä eikä nimestä Sini.

Yksinkertaistamisen ja laskutoimitusten helpottamiseksi vuoksi sovitaan että tällöin syntyy värähtelyä 100 Hz:n taajuudella (oikeasti kitaran paksuin kieli värähtelee taajuudella jonkin verran harvemmin). Tämä 100 Hz on se taajuus minkä korkeudella havaitsemme sävelen soivan eli se on tämän nuotin äänenkorkeus.

Kieli ei kuitenkaan värähtele ainoastaan koko pituudeltaan, vaan se jakautuu kahteen osaan, ja nämä molemmat puoliskot värähtelevät mukana.

Koska tämä värähtely on ”kaksinkertaista” verrattuna tuohon alkuperäiseen, sen taajuus on myös kaksinkertainen: 200 Hz. Kitaran kieli soi siis yhtä aikaa taajuuksilla 100 Hz ja 200 Hz. (Huom. asettamalla hiiren oikenpuoleisen kuvan päälle näet molempien värähtelytaajuuksien summan. Todellisuudessa kitaran kielestä lähtevien taajuuksien voimakkuussuhteet ovat erit kuin tässä esimerkissä, joten myös summa-aalto on erilainen.)

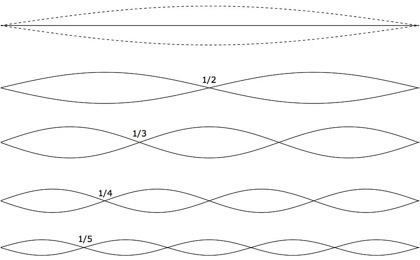
Homma ei lopu tähän: kieli jakautuu myös kolmeen osaan, neljään osaan, viiteen osaan yms. Ja kieli soi näillä kaikilla taajuuksilla yhtä aikaa.

Näin ollen tästä yhdestä kitaran kielestä lähteekin samanaikaisesti useita eri taajuuksia, jotka ovat kaikki tuon perusääneksen monikertoja: 200 Hz, 300 Hz, 400 Hz jne. Nämä monikerrat ovat nimeltään yläsäveliä, ja yhdessä perusääneksen kanssa ne muodostavat ns. yläsävelsarjan.

Näiden yläsävelten väliset voimakkuuserot ratkaisevat äänen värin, eli sen miltä ääni kuulostaa: onko kyseessä kitara, viulu, urku, piano, vaiko mies- tai naislaulajan a- tai o- vokaali. Äänenkorkeus taas määräytyy tuon perusääneksen taajuuden mukaan.

Itse asiassa kaikki äänet, joilla on jokin sävelkorkeus, voidaan tuottaa tällaisen yläsävelsarjan mukaan: perusääneksen lisäksi laitetaan noita monikertoja soimaan tarpeeksi monta yhtä aikaa sopivilla amplitudeilla niin saadaan aikaiseksi teoriassa minkä tahansa instrumentin ääni. Hälyäänet, joilla ei ole sävelkorkeutta (rummun iskut, pellit, kohina, räjähdys yms.), eivät perustu yläsävelsarjaan, vaan ne voivat sisältää mitä tahansa (ei-harmonisia) taajuuksia. Näissäkin tapauksissa noiden eri taajuuksilla tapahtuvien värähtelyjen voimakkuussuhteet määrittävät, miltä tämä häly kuulostaa, eli äänenväri perustuu siihen missä suhteessa mitäkin taajuuksia tämä värähtely sisältää.

Kunkin yläsävelen voimakkuus (amplitudi) ei luonnollisissa äänissä ole suinkaan stabiili, vaan se muuttuu ajan suhteen, esimerkiksi alla olevan animaation mukaisesti.

Todellisuudessa nämä amplitudit vaihtelevat paljon nopeammin ja monimutkaisemmin, mutta yllä oleva animaatio antaa kuvan siitä miten äänen taajuussisältö eli spektri vaihtelee ajan edetessä.

Yläsävelten merkitys

Yläsävelet määrittävät äänenvärin lisäksi suuren osan niistä ilmiöistä, joihin musiikki ja soittaminen perustuvat. Käyttämämme sävelet, intervallit ja asteikot johtuvat siitä, jopa soittimien rakennus ja jotkin laulu- ja soittotekniikat, kuten esim. huiluäänet.

Yllä olevasta nuottikuvasta löydät 16 ensimmäistä yläsäveltä. Koska nämä ovat ns. puhdasvireisiä intervalleja, eivät ne täysin vastaa niitä tasavireisiä nuotteja, joihin olemme tottuneet. Eniten tasavireisistä intervalleista poikkeavat nuotit on merkitty sulkeilla. Voi kuulla nämä yläsävelet yksi kerrallaan alla olevasta ääninäytteestä:

Eri viritysjärjestelmistä lisää luvussa zzz.

Tästä sarjasta voit löytää kaikki käyttämämme intervallit, alla olevasta kuvasta ja taulukosta löydät yleisimmät:

intervalli	yläsävelet mistä intervalli löytyy	taajuuksien suhdeluku
suuri sekunti	8. ja 7. yläsävel	8:7
pieni terssi	6. ja 5. yläsävel	6:5
suuri terssi	5. ja 4. yläsävel	5:4
kvartti	4. ja 3. yläsävel	4:3
kvintti	3. ja 2. yläsävel	3:2
pieni seksti	8. ja 5. yläsävel	8:5
pieni septimi	14. ja 8. yläsävel, myös 7. ja 4. sävel	7:4
suuri septimi	15. ja 8. yläsävel	15:8
oktaavi	2. ja 1. yläsävel (myös 4/2, 8/4 sekä 16/8)	2:1

Huomaa että intervallit ovat suhdelukuja: aina kun noustaan oktaavi ylöspäin, taajuus kaksinkertaistuu. Päästäksemme 100 Hz:n perusäänestä oktaavin ylöspäin täytyy taajuuteen lisätä 100 Hz (tavoite: 200 Hz). Jos haluamme päästä toisenkin oktaavin ylöspäin, nyt täytyy lisätä edellisen lisäksi vielä 200 Hz (400 Hz). Kolmanteen oktaaviin vaaditaan jo 400 Hz lisäystä (800 Hz), ja neljänteen 800 Hz (1600 Hz). Näin ollen: mitä korkeammalle mennään, sitä enemmän täytyy taajuuksia lisätä että saadaan aikaiseksi oktaavi.

Alla olevasta kuvasta näet, kuinka oktaavin "pituus" kasvaa joka kerta kaksinkertaiseksi.

Sama toimii myös toisinpäin: oktaavi alaspäin on aina puolet edellisestä taajuudesta. Niinpä 100 Hz/2 = 50 Hz on perusäänestämme oktaavi alaspäin, ja siitä seuraava oktaavi on 50 Hz/2=25 Hz.

Tämä on tärkeä huomio. Meidän korvamme ei ole äänenkorkeuden suhteen lineaarinen vaan logaritminen. Intervalleja ei voi siis laskea lisäämällä tiettyä määrä taajuuksia johonkin säveleen (esim. kiinteät 100 Hz), vaan taajuuksia täytyy lisätä tietyssä suhteessa. Joten mitä korkeammalle mennään, sitä suurempia hyppäyksiä täytyy hertsimäärällisesti tehdä saman intervallin aikaansaamiseksi. Esimerkin alin oktaavi on 25 Hz, ja ylin 3.200 Hz.

Asettamalla hiiren kuvan päälle näet logaritmisen ja lineaarisen funktion kuvaajat.